Mathematics | Mathematical analysis » Alapintegrálok

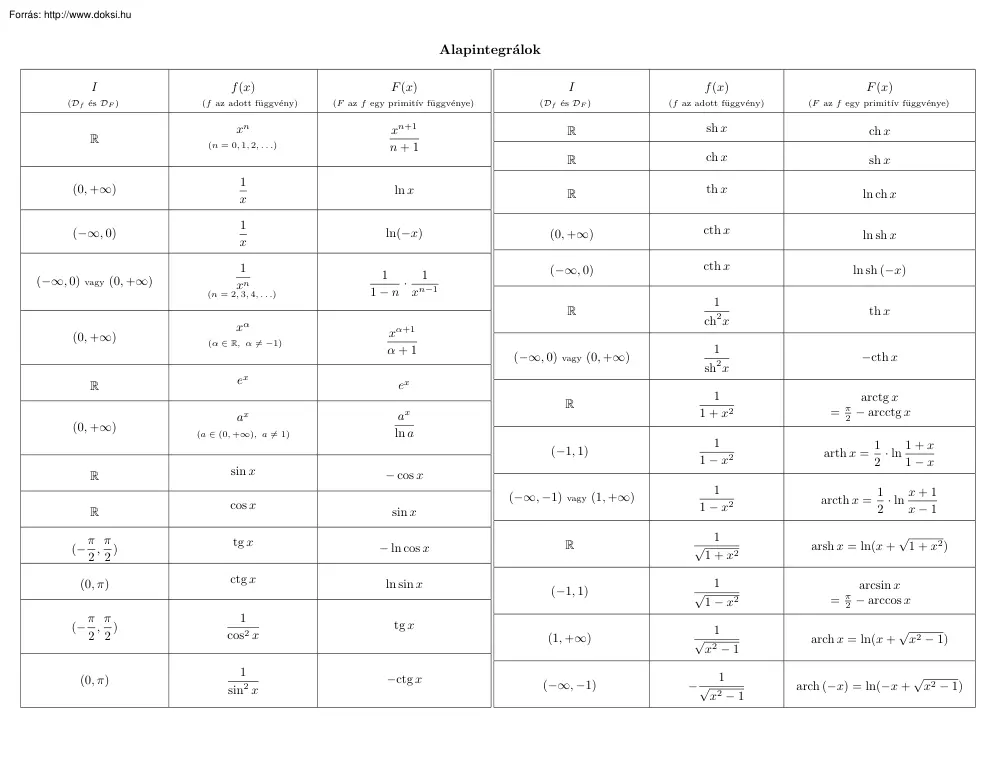
Alapintegrálok I (Df és DF ) R f (x) (f az adott függvény) xn (n = 0, 1, 2, . ) F (x) I f (x) F (x) (F az f egy primitı́v függvénye) (Df és DF ) (f az adott függvény) (F az f egy primitı́v függvénye) R sh x ch x R ch x sh x xn+1 n+1 (0, +∞) 1 x ln x R th x ln ch x (−∞, 0) 1 x ln(−x) (0, +∞) cth x ln sh x 1 xn 1 1 · 1 − n xn−1 (−∞, 0) cth x (−∞, 0) vagy (0, +∞) ln sh (−x) R 1 ch2 x th x (−∞, 0) vagy (0, +∞) 1 sh2 x −cth x R 1 1 + x2 arctg x = π2 − arcctg x (−1, 1) 1 1 − x2 arth x = 1+x 1 · ln 2 1−x (−∞, −1) vagy (1, +∞) 1 1 − x2 arcth x = x+1 1 · ln 2 x−1 arsh x = ln(x + (n = 2, 3, 4, . ) (0, +∞) R (0, +∞) R R xα (α ∈ R, α 6= −1) ex a x (a ∈ (0, +∞), a 6= 1) sin x cos x α+1 x α+1 ex x a ln a − cos x sin x π π (− , ) 2 2 tg x − ln cos x (0, π) ctg x ln sin x π π (− , ) 2 2 1 cos2 x tg x (0, π) 1

sin2 x −ctg x R √ 1 1 + x2 (−1, 1) √ 1 1 − x2 (1, +∞) √ (−∞, −1) −√ 1 x2 − 1 1 x2 − 1 √ 1 + x2 ) arcsin x = π2 − arccos x arch x = ln(x + √ x2 − 1) arch (−x) = ln(−x + √ x2 − 1)